Inverse Of Square Root Function

Finding the Inverse Office of a Square Root Function

To notice the inverse of a square root function, information technology is crucial to sketch or graph the given problem first to clearly place what the domain and range are. I volition utilize the domain and range of the original part to describe the domain and range of the changed function by interchanging them. If you demand additional information almost what I meant past "domain and range interchange" between the part and its inverse, meet my previous lesson near this.

Examples of How to Notice the Inverse of a Square Root Function

Instance one: Detect the inverse function, if it exists. State its domain and range.

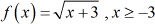
f(x) = sqrt of the quantity x+3 , x is greater than or equal to negative 3

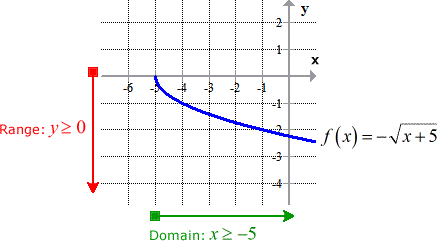
Every fourth dimension I come across a foursquare root part with a linear term inside the radical symbol, I always think of it every bit "half of a parabola" that is fatigued sideways. Since this is the positive case of the square root function, I am sure that its range will go increasingly more than positive, in plain words, skyrocket to positive infinity.

This particular square root function has this graph, with its domain and range identified.

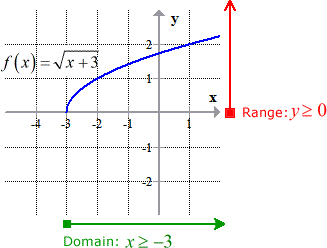
graph of f(x) = sqrt of the quantity x+3 where x is greater than or equal to -3 and y is greater than or equal to 0.

From this indicate, I volition have to solve for the changed algebraically by following the suggested steps. Basically, replace $\colour{red}f\left( 10 \right)$ by $\color{red}y$ , interchange $x$ and $y$ in the equation, solve for $y$ which soon will be replaced past the appropriate changed notation, and finally state the domain and range.

Remember to apply the techniques in solving radical equations to solve for the changed. Squaring or raising to the second power the foursquare root term should eliminate the radical. However, you must do it to both sides of the equation to continue it balanced.

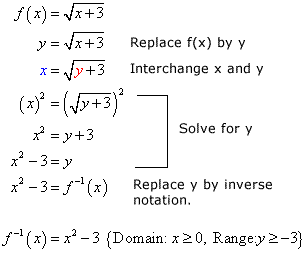
(f^-1)(x) = (x^2)-3; where x is greater than or equal to 0 and y is greater than or equal to -3.

Make certain that you lot verify the domain and range of the inverse role from the original part. They must be "contrary of each other".

Placing the graphs of the original function and its inverse in i coordinate axis.

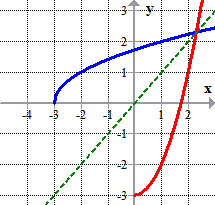
The graph of the original function, f(x) = sqrt of the quantity x+3, and its inverse, (f^-1)(x) = (x^2).

Tin yous encounter their symmetry along the line $y = ten$ ? See the dark-green dashed line.

Example two: Find the inverse office, if it exists. State its domain and range.

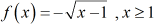
f(x) = negative sqrt of x minus 1; x is greater than or equal to 1

This function is the "bottom one-half" of a parabola because the square root function is negative. That negative symbol is simply $-one$ in disguise.

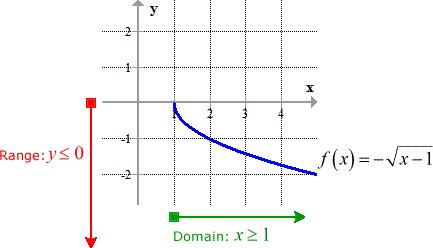
graph of f(x) = negative sqrt of x minus 1

In solving the equation, squaring both sides of the equation makes that $-ane$ "disappear" since ${\left( { - 1} \right)^2} = one$ . Its domain and range will be the swapped "version" of the original part.

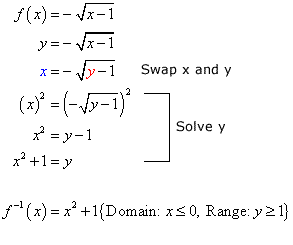
(f^-1)(x) = (x^2)+1 where x is less than or equal to 0 and y is greater than or equal to 1

Case three: Find the inverse function, if it exists. State its domain and range.

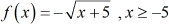
f(x) is equal to negative sqrt of x plus 5; x is greater than or equal to negative 5.

This is the graph of the original function showing both its domain and range.

Determining the range is usually a claiming. The best arroyo to find it is to use the graph of the given function with its domain. Analyze how the function behaves along the $y-$ axis while considering the x-values from the domain.

graph of f(x) is equal to negative sqrt of x plus 5

Here are the steps to solve or notice the inverse of the given square root part.

Every bit y'all tin can see, it'southward really simple. Brand sure that you do it carefully to prevent any unnecessary algebraic errors.

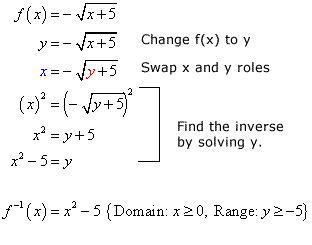
(f^-1)(x) = (x^2)-5 where x is greater than or equal to 0 and y is greater than or equal to negative 5

Example 4: Detect the inverse function, if information technology exists. State its domain and range.

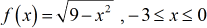
f(x) is equal to the sqrt of 9 minus x squared, x is greater than or equal to negative 3 and less than or equal to 0

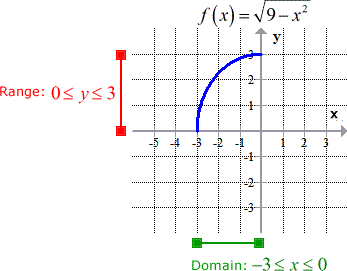
This office is one-fourth (quarter) of a circumvolve with radius $3$ located at Quadrant 2. Another manner of seeing it, this is one-half of the semi-circumvolve located in a higher place the horizontal axis.

I know that it will pass the horizontal line examination because no horizontal line will intersect it more than in one case. This is a adept candidate to have an changed part.

Again, I am able to easily draw the range because I have spent the time to graph it. Well, I promise that you realize the importance of having a visual assistance to assistance determine that "elusive" range.

The graph of f(x) is equal to the sqrt of 9 minus x squared.

The presence of a squared term inside the radical symbol tells me that I will employ the square root operation on both sides of the equation to observe the inverse. By doing so, I will have a plus or minus case. This is a situation where I will make a conclusion on which one to pick every bit the correct inverse role. Remember that inverse function is unique therefore I can't allow having ii answers.

How will I decide which ane to choose? The key is to consider the domain and range of the original function. I will bandy them to get the domain and range of the inverse function. Use this information to match which of the two candidate functions satisfy the required conditions.

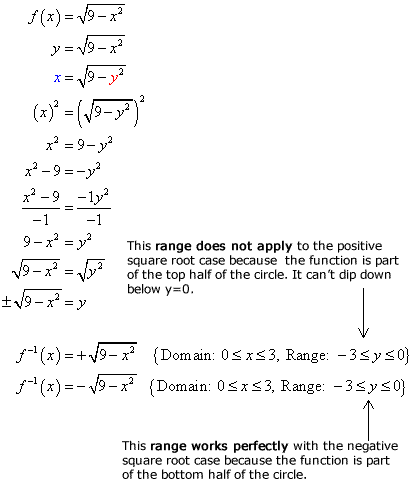
(f^-1)(x) = negative sqrt of 9 minus x squared where x is greater than or equal to 0 and less than or equal to 3, AND y is greater than or equal to negative 3 and less than or equal to 0

Although they have the same domain, the range hither is the "tie-breaker"! The range tells us that the inverse function has a minimum value of $y = -3$ and a maximum value of $y = 0$ .

The positive square root example fails this condition since it has a minimum at $y = 0$ and maximum at $y = 3$ . The negative case must be the obvious choice, fifty-fifty with further analysis.

Case v: Find the inverse function, if information technology exists. State its domain and range.

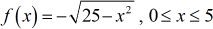
f(x) is equal to negative sqrt of 25 minus x squared, x is greater than or equal to 0 and less than or equal to 5

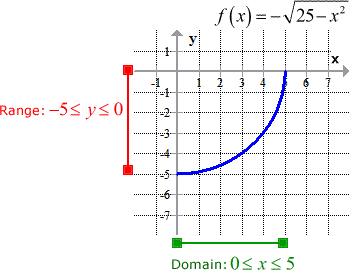
It's helpful to meet the graph of the original role considering we tin can hands effigy out both its domain and range.

The negative sign of the square root function implies that information technology is establish beneath the horizontal axis. Detect that this is similar to Case 4. It is also one-fourth of a circle only with a radius of $v$ . The domain forces the quarter circle to stay in Quadrant IV.

graph of f(x) is equal to negative sqrt of 25 minus x squared

This is how we discover its inverse algebraically.

Did you pick the right changed function out of the 2 possibilities? The reply is the case with the positive sign.

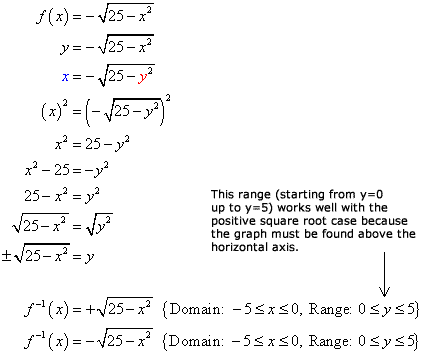
(f^-1)(x) = sqrt of 25 minus x squared where x is greater than or equal to negative 5 and less than or equal to 0 AND y is greater than or equal to 0 and less than or equal to 5

You lot might besides be interested in:

Changed of a 2×2 Matrix

Inverse of Absolute Value Function

Inverse of Constant Function

Inverse of Exponential Function

Inverse of Linear Part

Inverse of Logarithmic Office

Inverse of Quadratic Function

Changed of Rational Function