Opposite Angles In A Triangle

Equality of Reverse angles when Two sides of a Triangle are equal

Math Doubts
Geometry
Triangles
Properties

If two sides of a triangle are equal, then the angles opposite to the same 2 sides are also equal.

Introduction

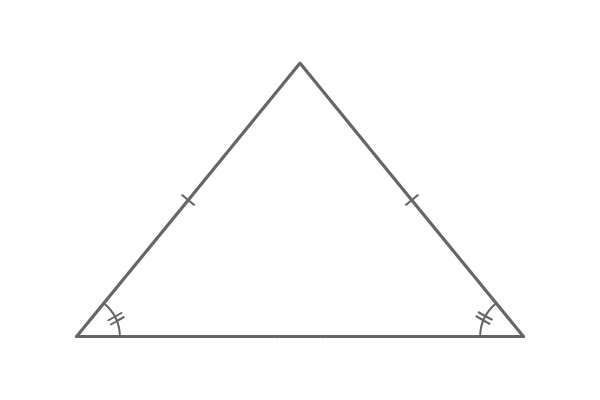
animation of isosceles triangle

The lengths of two sides in a triangle can be equal. Information technology is possible only in the case of both equilateral triangle and isosceles triangle.

Due to the equality holding of ii sides in the triangle, the angles that are contrary to them are likewise equal geometrically. This theorem can also be proved in geometry on the basis of symmetry belongings.

Therefore, it is cleared that the angles opposite to the two sides of equal length are equal in a triangle.

Proof

For proving this theorem, we have to construct either an equilateral or isosceles triangle.

animation to form isosceles triangle

$\Delta ABC$ is a triangle and its two sides are of equal length. Hence, the triangle $ABC$ is called an isosceles triangle. In this isosceles triangle, the lengths of the sides $\overline{Air-conditioning}$ and $\overline{BC}$ are equal.

$AC = BC$

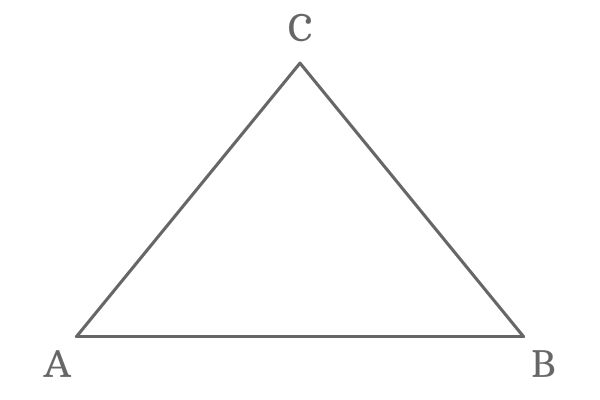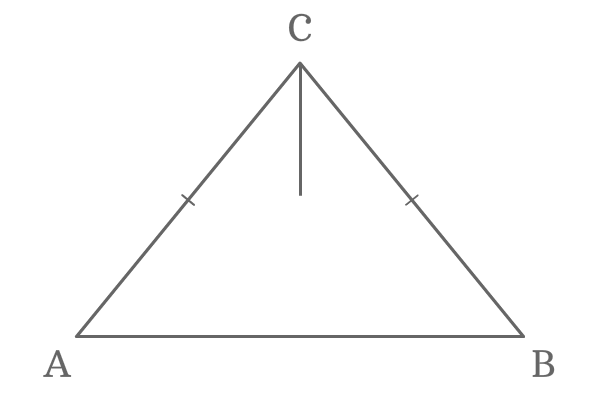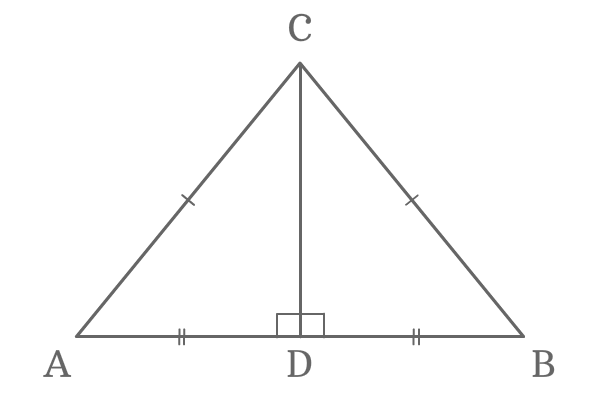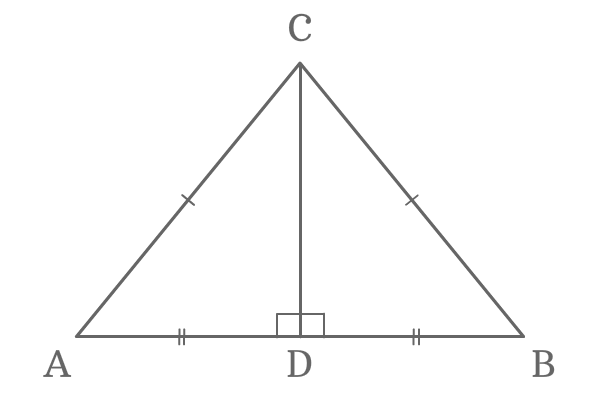
Draw a perpendicular line to the side $\overline{AB}$ from point $C$. It divides the side $\overline{AB}$ at its middle point exactly and the signal of intersection is $D$.

Therefore, $Advertisement = BD$.

Similarly, the line $\overline{DC}$ divides the $\Delta ABC$ as ii right angled triangles $\Delta DAC$ and $\Delta DBC$. Now, the perpendicular line $\overline{DC}$ is a mutual side to both right angled triangles.

congruent triangles

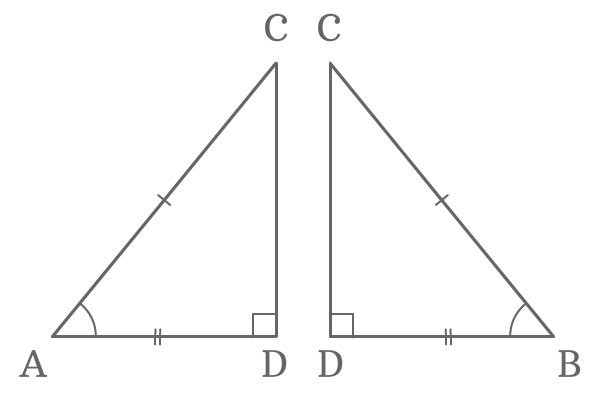
Now, compare the lengths of iii sides of both triangles.

$Ac = BC$
$AD = BD$
$DC = DC$

The comparison of lengths of sides of the both triangles revealed that the 2 triangles are same merely represented differently.

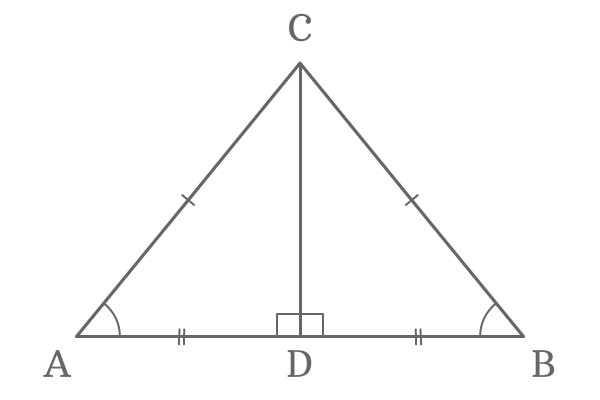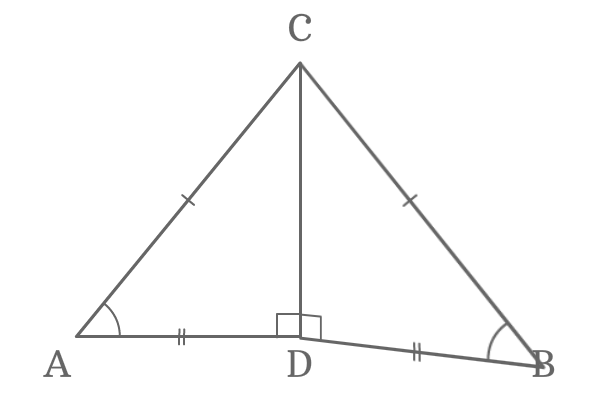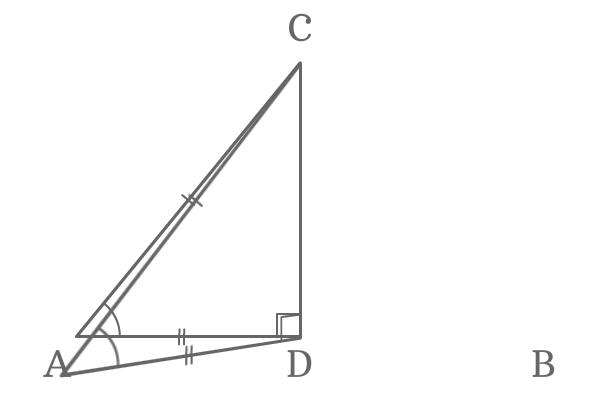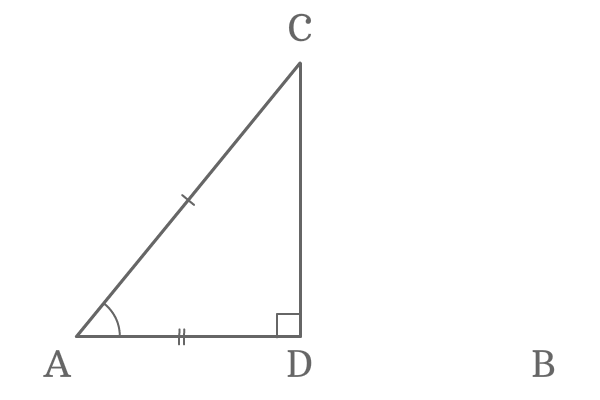
animation of congruency in isosceles triangle

Therefore, the $\Delta DAC$ and $\Delta DBC$ are known equally congruent triangles and they also correspond Right bending Hypotenuse side (RHS) criterion.

$\Delta DAC \cong \Delta DBC$

In this case, $\angle DAC$ is the opposite angle to the side $\overline{BC}$ and $\angle DBC$ is also opposite angle to the side $\overline{Air conditioning}$. The two angles are equals due to the congruency.

$\angle DAC = \angle DBC$

Therefore, if two sides of a triangle are equal, then the angles contrary to them are also equal.

Case

This property of the triangle tin can be proved geometrically by constructing a triangle but the lengths of any two sides of the triangle should be equal.

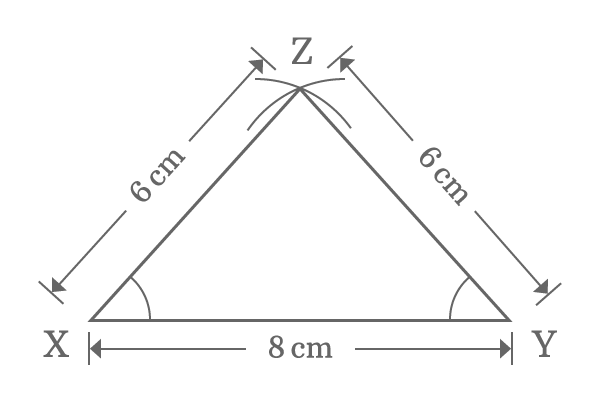
construction of isosceles triangle

Accept ruler and draw a directly line ($\overline{XY}$) of length $viii \, cm$ horizontally.

Use compass and fix distance between needle betoken and pencil point to $6 \, cm$. Depict an arc from point $X$ and also depict another arc from bespeak $Y$ but the arcs should be intersected. The intersecting point of both arcs is $Z$.

Join points $X$ and $Z$ and likewise join points $Y$ and $Z$ by a straight line using ruler. Thus, the $\Delta XYZ$ is synthetic geometrically.

$\angle XYZ$ and $\angle YXZ$ are opposite angles of the equal length sides $\overline{XZ}$ and $\overline{YZ}$ respectively. Now, measure the angles $XYZ$ and $YXZ$ by using protractor.

You practically observe that the $\angle XYZ$ and $\bending YXZ$ are equal and information technology is $48^\circ$ geometrically. Therefore, the angles opposite to the 2 equal length sides are equal geometrically.